Characteristics and Limitations

It is easy to take transformers for granted, because they have been with us since the early days of electricity. Perhaps their familiarity has rendered them less glamorous in comparison to more recently developed electronic and optical components and technologies. Nevertheless, transformers are a basic electrical component that we use often. Their ability to transform voltages, currents, and therefore impedances provide essential tools for the circuit designer. Here, we review how they work, and discuss a few of their more prominent limitations and characteristics. Similar issues apply to ferrite based magnetic components as well.

Conceptually, the transformer is a simple and elegant component resulting from the interaction of several of Maxwell's equations. Figure 1 shows an idealized transformer. Two sets of windings-call them #1 and #2, or input and output, or primary and secondary-are wound around a common magnetic core. If an AC voltage is imposed on one winding, resulting in current flow, Ampere's law tells us that magnetic flux will be generated. Because the core is magnetic, that is, possesses a permeability significantly greater than that of air or free space, virtually all of the flux stays in the core rather than spreading out, and is therefore linked through the turns of the second winding. Faraday's law tells us that the second winding will exhibit an output voltage determined by the rate of change of the magnetic flux passing through each turn of the secondary, multiplied by the number of turns (Figure 2).

Figure 1: A transformer is made from a pair of windings around a common core. It is modeled as a two-port circuit component.

Figure 2: The ratio of the number of turns in the windings determines the voltage and current ratios present in the windings. They go in opposite directions-if voltage is stepped up, current is stepped down, and vice-versa.

An ideal transformer will isolate the input circuit from the output circuit, transform the input voltage by the ratio of the number of turns in the windings, and be frequency independent. If the secondary has more turns than the primary, the voltage will be "stepped up"; if the secondary has fewer turns than the primary, the voltage will be "stepped down." The current will change in an inverse fashion. That is, if voltage is stepped up across a transformer, the current will be decreased by the same proportion. This is as it must be to conserve energy. The power that comes out of a transformer must equal the power that is put into it, less any losses due to such factors as magnetic imperfections and resistive heating of the transformer windings.

Practical Limitations The idealized transformer described above has only the transformation property-it doesn't have any losses, or power limitations. Its frequency response seems to be infinite. Real components have limited efficiency and bandwidth, and can act in a non-linear fashion. A circuit model incorporating these imperfections is shown in Figure 3. The imperfections are shown as equivalent components added to an ideal transformer.

Figure 3: Physical effects cause transformers to deviate from the simple idealized model. Shown is a small signal model which includes the effects of shunt and inter-winding capacitance, stray inductance, magnetic loss, and winding resistance. Note that under low frequency or large-signal conditions, the shunt primary inductance can become nonlinear if the transformer is driven into saturation.

These imperfections are caused by the physical effects listed below. Also indicated are the components to which they correspond in the circuit model of Figure 3.

Nonzero resistance of the windings (Rp and Rs) Frequency dependence of the material permeability Magnetic losses (Re) Intra-winding capacitance (turn to turn within a winding-Cp) Inter-winding capacitance (primary to secondary-Cps) Finite primary winding inductance (Le) Finite flux capability of the core material, leading to saturation (non-linear behavior of Le) Leakage inductance of the windings (Lp and Ls)

Let's review how these factors affect a transformer's operating characteristics. We'll take a quick overview, and then look at the effects due to saturation and winding resistance in more detail.

The resistance of the windings affects two important characteristics: power dissipation through heating, and impedance transformation (or equivalently, resistive voltage drop). Magnetic losses are of two main types. First, if the magnetic core is electrically conductive-e.g. an iron core-circulating electrical eddy currents induced by the magnetic fields will result in waste heating of the transformer core. Second, if the permeability of the core material is complex at the frequencies of interest, power will also be dissipated. The first effect is more important with low frequency power transformers (and is one reason that they are composed of laminated sections rather than monolithic bulk material), while the second occurs with ferrite materials. Both of these result in power loss through heating of the transformer core. Parasitic capacitances limit the upper bandwidth of operation and also reduce the isolation the transformer can provide. The inductance of the primary winding limits the low frequency operation of the transformer. There are two effects. For small signal operation, the core will not be saturated, but the transformer's performance will be limited by the low winding impedance. For large signal operation, the core will saturate, and the inductance will change during the course of a voltage cycle. This causes non-linear behavior, and can lead to catastrophic transformer failure.

Now, let's examine the problem of core saturation in more detail.

Of Transformers and Beads Power transformers and small signal ferrite inductors (beads, sleeves, and toroids) are both magnetic devices, although their applications are at opposite ends of the frequency and power spectrum. Power transformers and autotransformers are used in the laboratory to vary mains voltages to the levels required by different product types and regulatory jurisdictions, and to check product operation over specified variations. Ferrite beads, and their multi-turn cousins, common-mode and differential-mode chokes, are used to present frequency-selective barriers to unwanted high frequency signals ranging from approximately 100 kHz (for conducted emissions) to frequencies of several hundred MHz (for radiated emissions). Power transformers are large, and ferrite beads are relatively small, but both are affected by primary inductance limitations.

The operation of both types of devices is dramatically impaired when magnetic saturation of their cores occurs. Saturation lowers the incremental permeability (i.e., the change in flux, B, for an additional change in magnetizing force, H) of magnetic materials. Ferrite components for RF suppression applications are usually intended for use under small signal conditions. Transformers are inherently large signal devices. For both to operate as intended, it is essential to understand their magnetic limitations.

The key to understanding the operation of magnetic devices is the relationship between the current that is applied (I, in amperes), the resulting magnetic field (H, in amperes/meter), and the resulting magnetic flux (B, in tesla or webers/sq. meter). These in turn, determine the circuit parameters we usually work with, such as inductance and impedance.

Inductance (L) is defined as the instantaneous (or incremental) ratio of total magnetic flux linkage to applied current. The magnetic flux linkage is the flux in the magnetic core multiplied by the number of turns of wire that it passes through. This allows us to summarize a component's characteristics in the familiar circuit relation, V= L*di/dt. The inductance varies with the geometry of the core (mainly the cross-sectional area), the square of the number of turns, and varies in proportion to the permeability.

Operating on the B-H Curve For an isotropic magnetic material at low frequencies, the relationship between B and H, or permeability, is scalar. (At higher frequencies it becomes complex. The imaginary component shows up as a resistive loss, rather than contributing to inductance). However, the permeability in a magnetic material is not constant- the magnetic flux density B increases more and more slowly with increases in the applied magnetic field. That is, it saturates as a greater percentage of the internal magnetic domains are aligned with the applied field. This may be written with the formula:

B= µ (H) . H

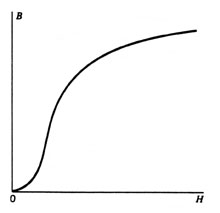
A typical B-H curve is shown in Figure 4. The slope of the curve decreases with increasing applied field. This means that the incremental, small signal permeability, and hence the primary winding inductance, decreases under large signal conditions. Since the inductance, as noted above, is proportional to the slope of the B-H curve, the inductance is not constant, but is instead a decreasing function of the current through the inductor. The magnetic inductor is only linear under small signal conditions.

Figure 4: A B-H curve for a magnetic material (hysteresis is ignored). The inductance is proportional to the derivative, or slope, of the B-H curve. When the material becomes fully magnetized, increasing the applied magnetic H-field has little effect on the resulting flux (B-field) in the material. The slope, and the inductance, approaches zero.

Circuit Effects of Saturation When power transformers saturate, their operation deteriorates in dramatic fashion. As Figure 5 shows, a simplified model for a power transformer consists of an ideal transformer, an allowance for the resistance of the windings, and a shunt primary inductance. Power transformers are inherently large signal, low frequency devices. Operation involves traversing along the B-H curve from one side to the other as the current and magnetizing H-field vary simultaneously.

Figure 5: Simplified equivalent circuit for a power transformer. When the core saturates, the primary inductance Lp drops to a very low value. Large currents flow through the primary winding, limited mostly by the winding resistance Rp. The secondary voltage Vout drops dramatically because of the decrease of the ratio of the rate of change of the linked flux to that of the input current.

As long as the core is not saturated and the primary inductance is large, everything works fine. But what happens when this is no longer the case? The relation for the current through the primary inductance is:

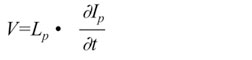We can integrate this to look at the current, noting explicitly that Lp is also a function of the instantaneous current, i, and that the applied voltage is sinusoidal:

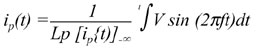If the current becomes large enough to saturate the core, the permeability drops to a very low value, and therefore, so does the inductance Lp of the transformer's primary. At this point, several things happen:

Very large currents flow The primary current, and the secondary voltage, become far from sinusoidal. The primary current gets very large for the balance of the half-cycle, and the secondary voltage drops from its initial sinusoidal shape to near zero. The transformer gets hot in a hurry, and consequences such as blown breakers and inoperative equipment usually follow.

It is important to realize that the saturation problem is a function of the applied voltage and frequency only. It is NOT caused by the amount of current drawn from the secondary winding.

If you are working with equipment destined for both the U. S. and international markets, you will need to generate and transform both 50 and 60 Hz power. A 50 Hz transformer will easily operate at 60 Hz, but it doesn't always work the other way around. I was surprised to find that many transformers and autotransformers ("variacs") sold in the United States are designed for use at 60 Hertz only. This means that you shouldn't be surprised if they act badly when you connect them to a 50 Hertz generator or solid state power source. You can use 60 Hertz transformers and variacs at 50 Hertz if you derate them by putting less voltage (about 20% less) across the primary, because then the current and internal H-fields build up to the saturation level more slowly. Of course, for a lot of testing you won't be derating them-you'll want them to operate at a higher than normal (e.g., for ITE, you would run at nominal +10% during a safety qualification test). You have to be careful - while some transformers are rated for 50/60 Hz operation, others are only rated for 60 Hz.

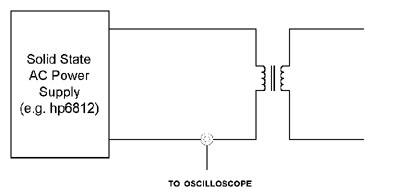
You can always check that you are in the range of healthy operation by placing a current clamp over the transformer primary and monitoring the current flow. If it is sinusoidal, saturation isn't occurring. As you lower the operating frequency below, or, alternatively, increase the primary voltage above, the stated operating parameters of the transformer, the primary current will develop a large hump as it saturates with each half cycle of the applied current. This current hump winds up dissipating in the winding resistance of the primary. Often, circuit breakers will pop. If a solid state AC source is available, you can easily check the extremes of useful voltage and frequency operation for your power transformers (see Figure 6).

Figure 6: You can check the actual extremes of voltage and frequency over which a transformer will operate with a solid state power source and a monitoring current clamp. Saturation of the core will cause large non-sinusoidal currents to flow.

We also note that saturation of a ferrite device will reduce its impedance. Typically this occurs because net DC current is applied rather than because of low-frequency AC operation. This can significantly reduce the ferrite's effectiveness as a high frequency suppression or coupling device (depending on whether it is a single bead, a common mode choke, or a high frequency signal transformer). The results will be less spectacular (no smoke) than for a power transformer because of the lower power involved.

Impedance Transformation Properties of Transformers

Another important characteristic of transformers is the way they transform impedances, and the deviation from ideal transformation that can be caused by winding (and wiring) resistance.

Consider an ideal transformer with winding 1 connected to an AC voltage source of value V1 and winding 2 connected to a resistive load of value R. The transformer has a turns ratio a= (n2/n1). Clearly, the voltage V2 across the resistor and the current I2 passing through it must be related to the input voltage and current by the turns ratio of the transformer. That is,

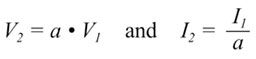But we know by Ohm's Law that, for the resistor, V2/I2=R. If we substitute the above relations into this equation and solve for V1/I1, we will get the impedance looking "into" the transformer from side 1. We find that

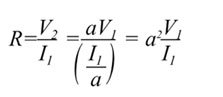which means that

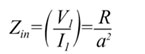Thus, a transformer transforms impedance by the square of the turns ratio. The higher impedance is seen on the side with the greater number of turns-the high voltage, low current side. Using our notation, if a>1, we are stepping up the source voltage, and the impedance seen at winding 1 of the transformer is lower than that of the load resistance across winding 2. If a<1, we are stepping down the source voltage, but the input impedance seen looking into winding 1 is higher than that of the load resistance. (See Figure 7)

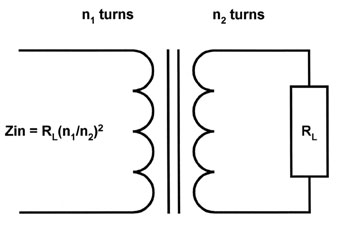Figure 7: A transformer transforms impedance as the square of the turns ratio because the voltage and current transformation ratios work in opposite directions.

We now give two examples of how impedance transformation and wiring/winding resistances interact. Our first example is large-signal - power distribution, while our second is drawn from small signal audio/telecom circuitry.

Impedance Transformation and Power Distribution The ability to transform voltages and impedances is one of the reasons that the AC voltage distribution system championed by Tesla and others won out over Edison's original DC system. In order to send electric power over long distances with useful efficiency, it is necessary to minimize the losses due to heating the power lines. That means that you want to transform the impedance of the load to a very high value over the transmission path, so the resistance of the transmission wires is a small fraction of the resistance of the total circuit. That's why we use high voltage transmission lines to carry power long distances and transform it locally to lower levels. (Figure 8). With AC power distribution, it is easy to change voltages with transformers as needed to minimize transmission loss.

Figure 8: Power transmission systems use high voltages and high impedances. This increases efficiency by minimizing the voltage drop across the transmission wires because the load is transformed up to a high impedance.

Resistance and Impedance Matching Calculations In small signal applications, such as in an audio or modem interface circuit, load matching, and hence the proper calculation of the impedance seen across a coupling transformer are important. Here, let's use a midband model which assumes that the main imperfection in the transformer is the resistance of both windings (Figure 9). Let's further assume that we are interested in creating an impedance which, seen from the load side, matches that of the load. This might be important in some telecommunications applications where a high return loss-that is, a good match to the line impedance-is desired to meet a performance or regulatory goal.

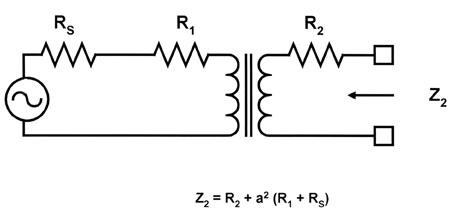Figure 9: In matching low level impedances, transformer winding resistance is significant. This figure shows the transformation viewed from the output side.

The transformer still transforms impedances with the square of the turns ratio, but we must account for the resistance of the windings. Let's assume that the turns ratio is still given by a = (n2/n1) The impedance seen from the load side (winding 2) becomes:

Z2 = a2 o (R1+Rs)+R2

As an example, if we had a 1:1 signal transformer with winding resistances R1 and R2 both equal to 100 ohms, we would have to set the source resistance Rs to 400 ohms. This seems straightforward enough, but note that the impedance seen looking into winding 1 is 800 ohms (the transformation of the 600 ohm load and the effect of the windings). Thus, looking at it from the primary side, we have a 400 ohm source driving an 800 ohm transformed load. This is unimportant, because the impedance that matters for low return loss is that seen looking into winding 2 from the load (or network) side. Here, we see a matched composite source (including the transformer) of 600 ohms driving our 600 ohm load.

Figure 10: A completed example where it is desired to select a source impedance which will cause a 1:1 transformer with 100 ohms resistance in each winding to present a 600 ohm matched termination to the telephone network. (a) If the driving voltage source (typically and op amp) impedance is set to 400 ohms, the desired impedance is seen looking in from the network side. (b) The network impedance presented at the input of the transformer, however, is 800 ohms. This alters the canceling gain required of a hybrid relative to the situation of zero winding resistance.

Summing Up Transformers are indispensable in power distribution as well as many circuit applications. Knowledge of how they work makes it easy to understand how to specify and use them effectively in circuit and laboratory applications.

top

transformers, current transformers, potential transformers, voltage transformers, motors, ac motors, dc motors, 2 stroke engines, two stroke engines, diesel engines, turbochargers, steam engines, rocket engines, manual transmissions, horsepower, gas turbine engines, fuel injection systems, car engines, car cooling systems